LightGBM核心技术：GOSS采样与直方图优化算法

Ch.2 LightGBM核心技术：GOSS采样与直方图优化算法

  在LGBM算法的计算流程中，当执行完特征压缩后，接下来就将进入到每棵树的建模过程中。不过同样是出于提高计算效率考虑，LGBM并不是带入全部数据进行每棵树的训练，而是采用了一种名为基于梯度的单边采样（Gradient-based One-Side Sampling，GOSS）的下采样方法，缩减实际带入模型训练的样本数量。这是一种非常特殊的采样方法，而其实践效果和EFB类似，都是能够在大幅提高计算效率的同时确保计算精度。并且，当已经完成了GOSS采样之后，在实际决策树生长过程中，LGBM也采用了XGB类似的直方图优化算法，来加速决策树的计算过程。从原理层面来看，LGBM和XGB的直方图优化算法并没有本质上的区别，只是二者在进行直方图计算时采用的指标略有不同，具体区别我们将在介绍直方图算法时具体讲解。此外，LGBM还在直方图的实际计算机计算层面进行了优化，例如Voting Parallel（投票特征并行）方法等。

  总的来说，本节我们将在上一小节数据处理结果基础上，进一步探讨LGBM算法中决策树模型的生长过程，该过程涉及到的核心算法包括GOSS抽样和直方图优化算法，本节我们仍然是理论结合手动实现的示例，来介绍这两个算法。首先导入上一小节处理好的数据data：

data = pd.read_csv('data.csv', index_col=0)
data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4
0	1.2	4.7	1	0	1	0.0	1.0	1.0
1	2.9	5.5	1	0	0	1.0	1.0	1.0
2	2.6	3.9	0	1	1	1.0	0.0	2.0
3	3.3	6.2	1	0	0	1.0	1.0	1.0
4	2.0	3.5	1	0	1	0.0	0.0	0.0
5	2.5	4.5	1	1	1	1.0	1.0	3.0
6	1.4	5.1	1	0	0	0.0	1.0	1.0
7	2.1	2.7	0	1	0	0.0	0.0	2.0
8	1.7	4.1	1	0	1	0.0	0.0	0.0
9	3.0	3.8	1	1	1	1.0	0.0	2.0

1.基于梯度的单边采样（Gradient-based One-Side Sampling，GOSS）

1.1 GOSS基本原理

  首先来看基于梯度的单边采样（Gradient-based One-Side Sampling）方法，也就是所谓的GOSS抽样方法。不同于简单随机抽样，GOSS是一种非常特殊的基于梯度分布的抽样方法。我们知道在执行优化算法的过程中，每个样本都有一个对应的梯度计算结果，如果某条样本梯度绝对值较小，则说明这条样本已经被正确的分类或者预测结果和真实结果非常接近，在后续的参数更新过程中，这些梯度绝对值较小的样本对参数的改进贡献较小，因此每次迭代计算时再把这些小梯度的样本再算一遍梯度，会一定程度造成资源浪费。而反观那些梯度绝对值较大的样本，这些样本具有更高的误差，因此对模型的训练有更大的贡献。因此GOSS的思路是将全部样本按照梯度绝对值大小进行降序排序，然后抽取梯度绝对值最大的前$a\%$的样本，然后把其他样本都视作小梯度样本，并从这些小梯度样本中随机抽取$b\%$个样本，而这些大梯度样本和随机抽取的小梯度样本，就构成了接下来模型训练的数据集。而只针对小梯度样本（一边）进行抽样、保留（另一边）全部大梯度样本，也就是单边采样一词的由来。

  而在具体执行GOSS的时候有以下几点需要注意：

• 1.GOSS计算过程是根据梯度的绝对值大小进行样本划分和抽样，并不是样本梯度的真实值；

• 2.GOSS中样本选取比例，也就是梯度绝对值最大的前$a\%$和小样本中随机抽样的$b\%$，实际上都是超参数，可以在建模过程中灵活调节。这里的$a\%$可以换成更专业的超参数名称：top_rate，而小样本抽取的$b\%$更专业的名称则是other_rate；

• 3.我们知道样本梯度是基于预测结果计算而来的（具体来说是损失函数的一阶导数），而在第一棵树构建之前我们就需要进行GOSS采样，此时还没有模型预测结果，梯度计算依据的是LGBM的初始预测值，和其他集成学习类似，LGBM的初始预测值也是根据损失函数的不同类型计算得到的结果；

• 4.由于每次迭代都会更新模型参数，因此每次建树之前都会重新进行抽样，而除非人为控制迭代过程（例如使用一种非常特殊的Booster API，后面会详细介绍），否则一般来说top_rate和other_rate设置好了就不会再发生变化；

• 5.关于top_rate和other_rate的数值设置，一般来说top_rate越大other_rate越小，则模型过拟合风险就越大，反之则模型学习能力会被限制，而如果这两个参数同时较大，则会增加模型训练复杂度，增加模型训练时间。关于这组参数，并没有一个普遍适用的取值，还是需要根据实际情况进行超参数优化。

• 6.尽管带入训练的数据是GOSS抽样后的数据，但在后续决策树生长的过程中，小梯度样本的梯度（和损失函数二阶导数）会再乘以一个大于1的膨胀系数，再和大梯度样本的梯度（和损失函数二阶导数）进行相加，构成一个数据集的梯度（和损失函数二阶导数），来指导后续的迭代进行。而之所以要让小梯度样本进一步膨胀再加入到样本数据梯度中，其实也是为了尽可能还原原始真实的数据集梯度。也即是说，GOSS抽样并不是想要改变数据集梯度，而是希望通过更小的计算量，来尽可能还原原始数据集完整梯度，以此来提升建模的精确度，其基本过程可以由下图进行表示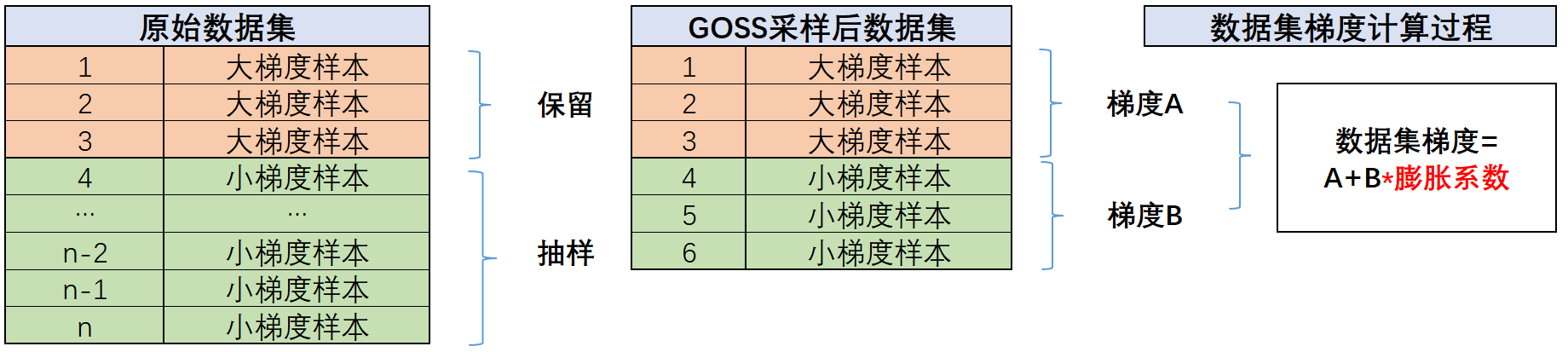：具体膨胀系数如何计算，其实也并不复杂，就是$\frac{1-a}{b}$，或者说是$\frac{1-top\_rate}{other\_rate}$。例如当top_rate=0.1，other_rate=0.2时，小样本梯度膨胀系数为：$\frac{1-top\_rate}{other\_rate}=\frac{1-0.1}{0.2}=4.5$。最终样本梯度=大样本梯度+小样本梯度*4.5算得。

• 7.GOSS过程带来的误差：最后需要注意的是，尽管GOSS抽样后我们通过膨胀系数来尽可能还原数据集整体的梯度，但这种还原肯定是存在一定误差的。根据原论文描述，这种误差可以通过如下公式进行表示：

  
  原论文中的公式并不好理解，这里我们可以将其等价为另一个公式进行解释。首先，假设我们有一个样本集合$I$，其中有$|I|$个样本。对于一个梯度值阈值$a$，我们将样本集合$I$划分为两个子集$I_{large}$和$I_{small}$。$I_{large}$包含所有梯度值大于等于$a$的样本，而$I_{small}$包含所有梯度值小于$a$的样本。用$|I_{large}|$表示$I_{large}$中的样本数量，用$|I_{small}|$表示$I_{small}$中的样本数量。接下来，我们从$I_{small}$中随机采样一定比例（$\alpha$）的样本，则梯度计算的最大误差估计为：$$\mathrm{Error} = \frac{1}{|I|}\sum_{i \in I_{large}} g_i - \frac{1 - \alpha}{\alpha |I_{small}|}\sum_{i \in I_{small}} g_i$$这里，$g_i$表示第$i$个样本的梯度值。

更多关于GOSS计算流程的介绍，我们将在后续手动示例中进行具体讨论

1.2 GOSS计算过程实例

• 损失函数、梯度与Hessian计算公式

  接下来我们继续借助简单示例数据集data来执行一次完整的GOSS采样计算过程。由于GOSS采样计算过程会涉及样本梯度计算，因此这里我们首先需要回顾样本梯度的计算方法。我们知道样本梯度是损失函数在各参数方向上求导得到的结果，因此梯度实际上和损失函数相关。这里data数据集是二分类数据集，因此假设建模过程中的损失函数是二分类交叉熵损失函数，在Lesson 4介绍梯度下降算法时，我们就介绍了二分类交叉熵损失函数的计算公式，以及样本梯度的计算方法，并借助手写代码来进行实现，这里我们快速回顾下交叉熵损失计算公式，对于第i条样本来说，$y_i$是真实标签，而$\hat y_i$或者$p_i$是概率预测结果，则样本整体二分类交叉熵损失计算公式如下：

$$\mathcal{L}=-\frac{1}{n} \sum_{i=1}^{n}\left[y_{i} \log p_{i}+\left(1-y_{i}\right) \log \left(1-p_{i}\right)\right]$$

此时第$i$条样本的梯度就是损失函数对预测样本的一阶偏导数：

$$\frac{\partial \mathcal{L}}{\partial p_{i}}=\frac{1-y_{i}}{1-p_{i}}-\frac{y_{i}}{p_{i}}$$

更进一步的，由于后续直方图计算过程还需要用到损失函数的二阶偏导数，也就是所谓的Hessian矩阵（值），也被称作黑塞矩阵、海森矩阵等。对于第$i$条样本，损失函数的二阶偏导数计算公式如下：

$$\frac{\partial^{2} \mathcal{L}}{\partial p_{i}^{2}}=\frac{y_{i}}{p_{i}^{2}}+\frac{1-y_{i}}{\left(1-p_{i}\right)^{2}}$$

并且，为了方便后续计算，我们可以编写函数来进行损失函数、梯度和Hessian值的计算。其中二分类交叉熵损失可以按照如下方式进行计算：

def binary_cross_entropy(y_true, y_pred):
    """
    计算二分类交叉熵损失函数
    :param y_true: 真实标签，一个 Numpy 数组，形状为 (n_samples,)
    :param y_pred: 预测标签，一个 Numpy 数组，形状为 (n_samples,)
    :return:二分类交叉熵损失值，一个标量
    """
    # 确保输入的标签为 0 或 1
    y_true = np.clip(y_true, 1e-7, 1-1e-7)
    y_pred = np.clip(y_pred, 1e-7, 1-1e-7)
    # 计算二分类交叉熵损失
    loss = -(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)).mean()
    return loss

这里的np.clip函数是用于将输出结果限制在一个范围内，避免出现零值相除的情况（sklearn中用于实现相同功能的log_loss函数也是采用类似的处理方法）。而每条样本的梯度计算函数如下：

def binary_cross_entropy_grad(y_true, y_pred):
    """
    计算二分类交叉熵损失函数的一阶导数
    :param y_true: 真实标签，一个 Numpy 数组，形状为 (n_samples,)
    :param y_pred: 预测标签，一个 Numpy 数组，形状为 (n_samples,)
    :return:二分类交叉熵损失函数的一阶导数，一个 Numpy 数组，形状为 (n_samples,)
    """
    # 确保输入的标签为 0 或 1
    y_true = np.clip(y_true, 1e-7, 1-1e-7)
    y_pred = np.clip(y_pred, 1e-7, 1-1e-7)
    # 计算二分类交叉熵损失函数的一阶导数
    grad = (1 - y_true) / (1 - y_pred) - y_true / y_pred
    return grad

每条样本的Hessian值计算函数如下：

def binary_cross_entropy_hess(y_true, y_pred):
    """
    计算二分类交叉熵损失函数的二阶导数
    :param y_true: 真实标签，一个 Numpy 数组，形状为 (n_samples,)
    :param y_pred: 预测标签，一个 Numpy 数组，形状为 (n_samples,)
    :return: 生成的特征张和标签张量：二分类交叉熵损失函数的二阶导数，一个 Numpy 数组，形状为 (n_samples,)
    """
    # 确保输入的标签为 0 或 1
    y_true = np.clip(y_true, 1e-7, 1 - 1e-7)
    y_pred = np.clip(y_pred, 1e-7, 1 - 1e-7)
    # 计算二分类交叉熵损失函数的二阶导数
    hess = y_true / (y_pred ** 2) + (1 - y_true) / ((1 - y_pred) ** 2)
    return hess

有了这些函数定义后，接下来我们来查看当前数据集在首次建模之前的梯度值如何计算。

• LGBM初始预测值

  正如此前所说，首次进行GOSS抽样时梯度计算依据是LGBM算法的初始预测值，如果是交叉熵损失函数，则初始预测值为1类样本占比（或者1类样本总数）的对数几率（log odds）计算结果，并且每条样本初始预测值都相同，具体计算过程可以由如下计算公式表示：

$$\hat y = ln\frac{p}{1-p}$$

其中$p$为1类的占比（或者1类总数，计算结果都相同）。例如对于data数据集来说，初始预测值可以按照如下方式进行计算：

data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4
0	1.2	4.7	1	0	1	0.0	1.0	1.0
1	2.9	5.5	1	0	0	1.0	1.0	1.0
2	2.6	3.9	0	1	1	1.0	0.0	2.0
3	3.3	6.2	1	0	0	1.0	1.0	1.0
4	2.0	3.5	1	0	1	0.0	0.0	0.0
5	2.5	4.5	1	1	1	1.0	1.0	3.0
6	1.4	5.1	1	0	0	0.0	1.0	1.0
7	2.1	2.7	0	1	0	0.0	0.0	2.0
8	1.7	4.1	1	0	1	0.0	0.0	0.0
9	3.0	3.8	1	1	1	1.0	0.0	2.0

# 计算每个类别的频率
class_freq = data['y'].value_counts(normalize=True)

# 计算初始预测值
initial_prediction = np.log(class_freq[1] / class_freq[0])

print("初始预测值：", initial_prediction)

初始预测值： 0.4054651081081642

class_freq

1    0.6
0    0.4
Name: y, dtype: float64

class_freq[1]

0.6

因此所有样本的初始预测结果为0.4，将其添加到data的最后一列中：

y_pred = np.array([0.4054]*10)
y_pred

array([0.4054, 0.4054, 0.4054, 0.4054, 0.4054, 0.4054, 0.4054, 0.4054,
       0.4054, 0.4054])

data['y_pred'] = y_pred
data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred
0	1.2	4.7	1	0	1	0.0	1.0	1.0	0.4054
1	2.9	5.5	1	0	0	1.0	1.0	1.0	0.4054
2	2.6	3.9	0	1	1	1.0	0.0	2.0	0.4054
3	3.3	6.2	1	0	0	1.0	1.0	1.0	0.4054
4	2.0	3.5	1	0	1	0.0	0.0	0.0	0.4054
5	2.5	4.5	1	1	1	1.0	1.0	3.0	0.4054
6	1.4	5.1	1	0	0	0.0	1.0	1.0	0.4054
7	2.1	2.7	0	1	0	0.0	0.0	2.0	0.4054
8	1.7	4.1	1	0	1	0.0	0.0	0.0	0.4054
9	3.0	3.8	1	1	1	1.0	0.0	2.0	0.4054

接下来我们即可依据y_pred来计算每条样本的梯度。

• 样本梯度与hes值计算

  这里我们借助刚才定义的binary_cross_entropy_grad函数进行样本梯度计算：

binary_cross_entropy_grad(data['y'], data['y_pred'])

0   -2.466699
1    1.681802
2   -2.466699
3    1.681802
4   -2.466699
5   -2.466699
6    1.681802
7    1.681802
8   -2.466699
9   -2.466699
dtype: float64

并将其追加到data数据集中：

data['grad'] = binary_cross_entropy_grad(data['y'], data['y_pred'])
data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad
0	1.2	4.7	1	0	1	0.0	1.0	1.0	0.4054	-2.466699
1	2.9	5.5	1	0	0	1.0	1.0	1.0	0.4054	1.681802
2	2.6	3.9	0	1	1	1.0	0.0	2.0	0.4054	-2.466699
3	3.3	6.2	1	0	0	1.0	1.0	1.0	0.4054	1.681802
4	2.0	3.5	1	0	1	0.0	0.0	0.0	0.4054	-2.466699
5	2.5	4.5	1	1	1	1.0	1.0	3.0	0.4054	-2.466699
6	1.4	5.1	1	0	0	0.0	1.0	1.0	0.4054	1.681802
7	2.1	2.7	0	1	0	0.0	0.0	2.0	0.4054	1.681802
8	1.7	4.1	1	0	1	0.0	0.0	0.0	0.4054	-2.466699
9	3.0	3.8	1	1	1	1.0	0.0	2.0	0.4054	-2.466699

然后再计算样本的hes值：

binary_cross_entropy_hess(data['y'], data['y_pred'])

0    6.084606
1    2.828461
2    6.084606
3    2.828461
4    6.084606
5    6.084606
6    2.828461
7    2.828461
8    6.084606
9    6.084606
dtype: float64

data['hess'] = binary_cross_entropy_hess(data['y'], data['y_pred'])
data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad	hess
0	1.2	4.7	1	0	1	0.0	1.0	1.0	0.4054	-2.466699	6.084606
1	2.9	5.5	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461
2	2.6	3.9	0	1	1	1.0	0.0	2.0	0.4054	-2.466699	6.084606
3	3.3	6.2	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461
4	2.0	3.5	1	0	1	0.0	0.0	0.0	0.4054	-2.466699	6.084606
5	2.5	4.5	1	1	1	1.0	1.0	3.0	0.4054	-2.466699	6.084606
6	1.4	5.1	1	0	0	0.0	1.0	1.0	0.4054	1.681802	2.828461
7	2.1	2.7	0	1	0	0.0	0.0	2.0	0.4054	1.681802	2.828461
8	1.7	4.1	1	0	1	0.0	0.0	0.0	0.4054	-2.466699	6.084606
9	3.0	3.8	1	1	1	1.0	0.0	2.0	0.4054	-2.466699	6.084606

• GOSS抽样

  据此我们即可进一步执行GOSS抽样。这里我们假设top_rate=0.2，other_rate=0.5，由于我们样本量较少，因此这里设置的比例偏大。此时GOSS抽样过程如下，首先计算样本梯度绝对值：

abs_gradients = np.abs(data['grad'])
abs_gradients

0    2.466699
1    1.681802
2    2.466699
3    1.681802
4    2.466699
5    2.466699
6    1.681802
7    1.681802
8    2.466699
9    2.466699
Name: grad, dtype: float64

然后进行从大到小的索引排序：

sorted_index = np.argsort(-abs_gradients)
sorted_index

0    0
1    2
2    4
3    5
4    8
5    9
6    1
7    3
8    6
9    7
Name: grad, dtype: int64

此时top_rate=0.2，other_rate=0.5，即从10条数据中挑选出梯度最大的2条数据，然后从剩下的8条数据中抽取50%，即抽取4条数据，共同构成本次GOSS抽样得到的训练数据集。这里我们先借助布尔索引先挑选出梯度最大的2条数据：

topn_index = sorted_index[:2]
topn_index.values

array([0, 2], dtype=int64)

两条数据抽取结果如下：

topn_data = data.iloc[topn_index.values, :]
topn_data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad	hess
0	1.2	4.7	1	0	1	0.0	1.0	1.0	0.4054	-2.466699	6.084606
2	2.6	3.9	0	1	1	1.0	0.0	2.0	0.4054	-2.466699	6.084606

然后再从剩下的数据集中随机抽取4条数据，首先是找到剩余数据集索引：

sorted_index >= 2

0    False
1     True
2     True
3     True
4     True
5     True
6    False
7     True
8     True
9     True
Name: grad, dtype: bool

data[sorted_index >= 2].index

Int64Index([1, 2, 3, 4, 5, 7, 8, 9], dtype='int64')

然后进行抽样，这里采用无放回抽样，并提前设置好随机数种子：

np.random.seed(12)
raten_index = np.random.choice(data[sorted_index >= 2].index, size=4, replace=False)
raten_index

array([5, 8, 1, 3], dtype=int64)

raten_data = data.iloc[raten_index, :]
raten_data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad	hess
5	2.5	4.5	1	1	1	1.0	1.0	3.0	0.4054	-2.466699	6.084606
8	1.7	4.1	1	0	1	0.0	0.0	0.0	0.4054	-2.466699	6.084606
1	2.9	5.5	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461
3	3.3	6.2	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461

至此，我们就完成了一次GOSS抽样全过程，接下来我们就将带入我们抽样得到的topn_data和raten_data带入进行模型训练。

需要注意的是，这里实现的GOSS抽样的代码流程并不是LGBM源码实现流程，源码的计算过程会更加高效且大都由C++编写。

2.LGBM决策树生长过程与直方图优化算法（Histogram-based Algorithm）

  在拿到GOSS抽样的数据集之后，接下来就正式进入到单独一颗决策树的生长过程中。该过程将涉及三个核心概念，LGBM决策树生长的增益计算公式、Leaf wise tree growth（叶节点优先）生长策略以及直方图优化算法。接下来我们逐一对其进行介绍。

2.1 基本原理介绍

• 直方图优化算法（Histogram-based Algorithm）

  直方图优化算法与其说是一种算法，不如是一种决策树生长分裂过程中数据集（及其关键信息）的表示方法——即通过直方图来表示数据集（及其关键信息）在决策树生长过程中的分裂即计算过程。这种表示方法能够大幅减少数据集内存占用、提升计算速度，并且方便进行直方图差分计算——子节点的直方图可以通过从父节点的直方图中减去兄弟节点的直方图来得到。

  需要注意的是，直方图算法最早是XGB算法提出的一种加速计算的方法，LGBM和XGB的直方图算法在直方图的表示形式上并没有任何区别，只是在直方图统计的值方面有区别：XGB是用直方图统计样本值的累加（并对特征进行排序），而LGBM是用直方图统计数据集的一阶导数和Hessian值的累加（并对特征进行排序）。也正因如此，LGBM可以利用直方图进行差分加速，而XGB不行。从这点而言，LGBM的直方图优化算法可以视作XGB直方图优化算法的优化版本。当然除此之外，LGBM还有很多并行计算的策略，进一步加速其计算过程。

• LGBM决策树生长的增益计算公式

  而在具体的决策树生长过程中，最重要的是进行切分点的选取，这个过程中最重要的分裂增益的计算方法。不同于CART树的基于基尼系数差的增益计算方法和C4.5的基于信息熵的信息增益，LGBM采用了一种非常特殊的、同时包含梯度和Hessian值得分裂增益计算方法，具体计算公式如下：

$$Gain = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \alpha \cdot (|w_L|+|w_R|)$$

其中，$G_L$ 和 $G_R$ 分别左节点和右节点的梯度和，$H_L$ 和 $H_R$ 分别是左节点和右节点的Hessian和，$\lambda$ 是 reg_lambda 参数（L2正则化项），$\alpha$ 是 reg_alpha 参数（L1正则化项），$w_L$ 和 $w_R$ 分别是左节点和右节点的权重。并且，对于一个节点，权重计算公式如下：

$$w=-\frac{G}{H+\lambda}$$

而对于reg_alpha和reg_lambda，其实是模型的两个超参数，也被称作L1正则化参数和L2正则化参数，用于控制模型结构风险。根据分裂增益计算公式不难看出，在数据集梯度和Hessian固定不变的情况下，L1正则化参数和L2正则化参数取值越大，增益计算结果就越小，决策树就越倾向于不分裂。

这里需要注意的是，LGBM分裂增益计算公式有三个不同的版本，原始论文、官网和源码实现过程分别给出了三种不同的分裂增益计算公式。本节列举的分裂增益计算公式是根据源码公式推导而来，下一小节我们将围绕此问题进行详细的讨论。

• LGBM的Leaf wise tree growth生长策略

  在具体生长的过程中，LGBM中的决策树也是同样会比较不同切分点带来的增益，然后选择增益最大的切分点进行分裂，这个过程和其他所有决策树都一样。而所谓的Leaf wise tree growth（叶节点优先）生长策略，则是对比另一种生长策略：Level-wise tree growth（层次优先的生长策略），前者是一次生长一个节点，可以长成不同子树深浅不一的决策树：

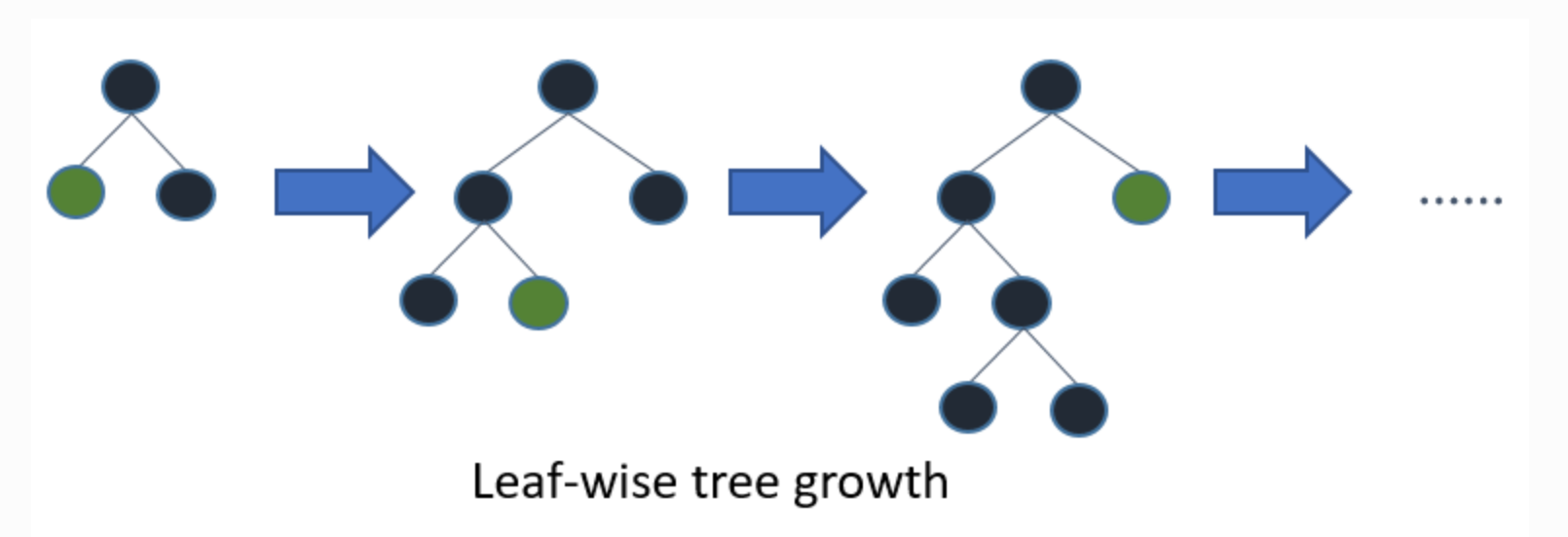
而Level-wise tree growth则是一次生长一层，最后决策树将是左右子树深度：

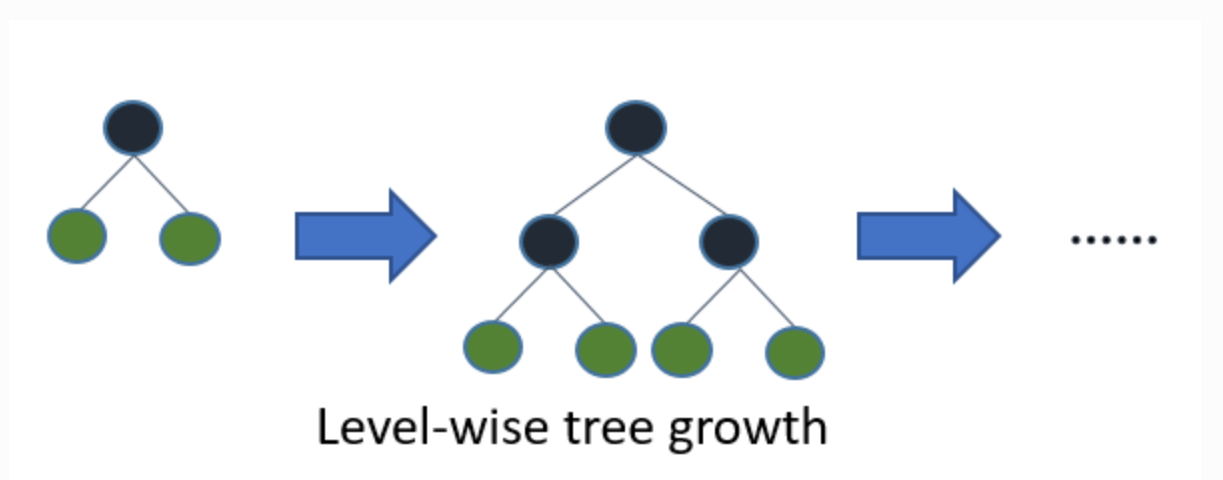
  其实关于这两种不同的生长方式，大家可以回顾Lesson 8决策树的相关内容，其中CART树就是一种Leaf wise tree growth，而C3.0就是Level-wise tree growth，这里我们可以理解为LGBM就是采用了CART树类似的生长流程即可。相比层次优先的生长策略，叶节点优先的生长策略会耗费更多的计算量、但同时也会有更高的预测精度。对于其他大多数集成学习算法来说，为了提高计算效率，其实都是采用的层次优先的生长策略（比如XGB），而LGBM经过了一系列数据压缩和其他优化方法，本来就拥有非常高的计算效率，因此在具体决策树建模的时候采用了一种更高精度叶节点优先的策略，来确保其在压缩后的数据上能够获得更高的预测精度。

  当然，叶节点优先的生长策略也会增加模型过拟合风险，因此对于LGBM来说，必须要通过限制树的最大深度来解决叶节点优先带来的过拟合问题，因此，对于LGBM来说，在超参数优化时树的最大深度max_depth将会是一个非常重要的超参数。

2.2 手动实现流程

  接下来，我们结合data数据集及之前抽样得到的GOSS数据集，来手动执行决策树生长流程。这里我们首先介绍如何手动计算一颗树的生长流程，然后再介绍如何采用直方图算法来优化这个计算流程。这里需要注意的是，实际的LGBM在进行迭代时是围绕伪残差进行拟合，这里为了便于介绍决策树的分裂增益和Leaf wise tree growth生长策略，决策树拟合目标改为数据集标签。在下一小节，我们将详细讨论LGBM伪残差计算公式以及如何围绕伪残差进行决策树建模拟合。

• 数据准备

  首先准备手动计算所需数据集，还是围绕此前介绍的data数据集，我们将GOSS抽样得到的数据集进行合并和标记处理。

data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad	hess
0	1.2	4.7	1	0	1	0.0	1.0	1.0	0.4054	-2.466699	6.084606
1	2.9	5.5	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461
2	2.6	3.9	0	1	1	1.0	0.0	2.0	0.4054	-2.466699	6.084606
3	3.3	6.2	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461
4	2.0	3.5	1	0	1	0.0	0.0	0.0	0.4054	-2.466699	6.084606
5	2.5	4.5	1	1	1	1.0	1.0	3.0	0.4054	-2.466699	6.084606
6	1.4	5.1	1	0	0	0.0	1.0	1.0	0.4054	1.681802	2.828461
7	2.1	2.7	0	1	0	0.0	0.0	2.0	0.4054	1.681802	2.828461
8	1.7	4.1	1	0	1	0.0	0.0	0.0	0.4054	-2.466699	6.084606
9	3.0	3.8	1	1	1	1.0	0.0	2.0	0.4054	-2.466699	6.084606

抽样得到的数据集如下：

topn_data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad	hess
0	1.2	4.7	1	0	1	0.0	1.0	1.0	0.4054	-2.466699	6.084606
2	2.6	3.9	0	1	1	1.0	0.0	2.0	0.4054	-2.466699	6.084606

raten_data

	x1	x2	x3	x4	y	x1_binned	x2_binned	x2_binned&x4	y_pred	grad	hess
5	2.5	4.5	1	1	1	1.0	1.0	3.0	0.4054	-2.466699	6.084606
8	1.7	4.1	1	0	1	0.0	0.0	0.0	0.4054	-2.466699	6.084606
1	2.9	5.5	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461
3	3.3	6.2	1	0	0	1.0	1.0	1.0	0.4054	1.681802	2.828461

这里我们将抽样得到的数据集进行拼接，只保留经过分箱和EFB剩下的特征，并保留标签、梯度和hess值:

data_goss = pd.concat([topn_data, raten_data], axis=0)[['x1_binned', 'x2_binned&x4', 'x3', 'y', 'grad', 'hess']]
data_goss

	x1_binned	x2_binned&x4	x3	y	grad	hess
0	0.0	1.0	1	1	-2.466699	6.084606
2	1.0	2.0	0	1	-2.466699	6.084606
5	1.0	3.0	1	1	-2.466699	6.084606
8	0.0	0.0	1	1	-2.466699	6.084606
1	1.0	1.0	1	0	1.681802	2.828461
3	1.0	1.0	1	0	1.681802	2.828461

然后新增一个topn二分类变量，用于标记是否是大梯度样本，大梯度样本用1表示，小梯度样本用0标记：

data_goss['topn'] = [1, 1, 0, 0, 0, 0,]
data_goss

	x1_binned	x2_binned&x4	x3	y	grad	hess	topn
0	0.0	1.0	1	1	-2.466699	6.084606	1
2	1.0	2.0	0	1	-2.466699	6.084606	1
5	1.0	3.0	1	1	-2.466699	6.084606	0
8	0.0	0.0	1	1	-2.466699	6.084606	0
1	1.0	1.0	1	0	1.681802	2.828461	0
3	1.0	1.0	1	0	1.681802	2.828461	0

data_goss.to_csv('data_goss.csv')

• 决策树的第一层分裂

  接下来，我们尝试进行决策树的生长过程计算。由于现在数据集中只有x1_binned、x2_binned&x4和x3三个离散变量，因此不难发现，备选的切分点只有x1_binned=0.5、x2_binned&x4=0.5、x2_binned&x4=1.5、x2_binned&x4=2.5和x3=0.5五个，因此我们需要分别计算这5个不同切分点取值下决策树分裂的增益，然后选取增益最大的切分点进行切分，从而完成这次的决策树生长。

  我们先以x1_binned=0.5为切分点计算分裂增益。根据此前介绍，LGBM决策树分裂过程中的增益计算公式如下：

$$Gain = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \alpha \cdot (|w_L|+|w_R|)$$

其中，$G_L$ 和 $G_R$ 分别左节点和右节点的梯度和，$H_L$ 和 $H_R$ 分别是左节点和右节点的Hessian和，$\lambda$ 是 reg_lambda 参数（L2正则化项），$\alpha$ 是 reg_alpha 参数（L1正则化项），$w_L$ 和 $w_R$ 分别是左节点和右节点的权重。并且，对于一个节点，权重计算公式如下：

$$w=-\frac{G}{H+\lambda}$$

同时，$\frac{G_L^2}{H_L + \lambda}$、$\frac{G_R^2}{H_R + \lambda}$分别也可以看成是左、右节点的标签不纯度计算指标，$\frac{(G_L + G_R)^2}{H_L + H_R + \lambda}$也可以看成是父节点的标签不纯度计算指标，该计算公式和XGB算法的结构分数计算公式完全相同。而不同的是在LGBM的决策树生长过程中，还有一个用于控制整体复杂度的L1正则化项，用于乘以左右节点的权重绝对值之和，作为增益的惩罚项。这里需要注意，XGB中也有叶节点权重的概念，且XGB的叶节点权重和LGBM叶节点权重计算公式完全一致。

这里我们假设$\alpha=0.02$，$\lambda=0.1$，则在x1_binned=0.5为切分点时数据集分裂情况如下：

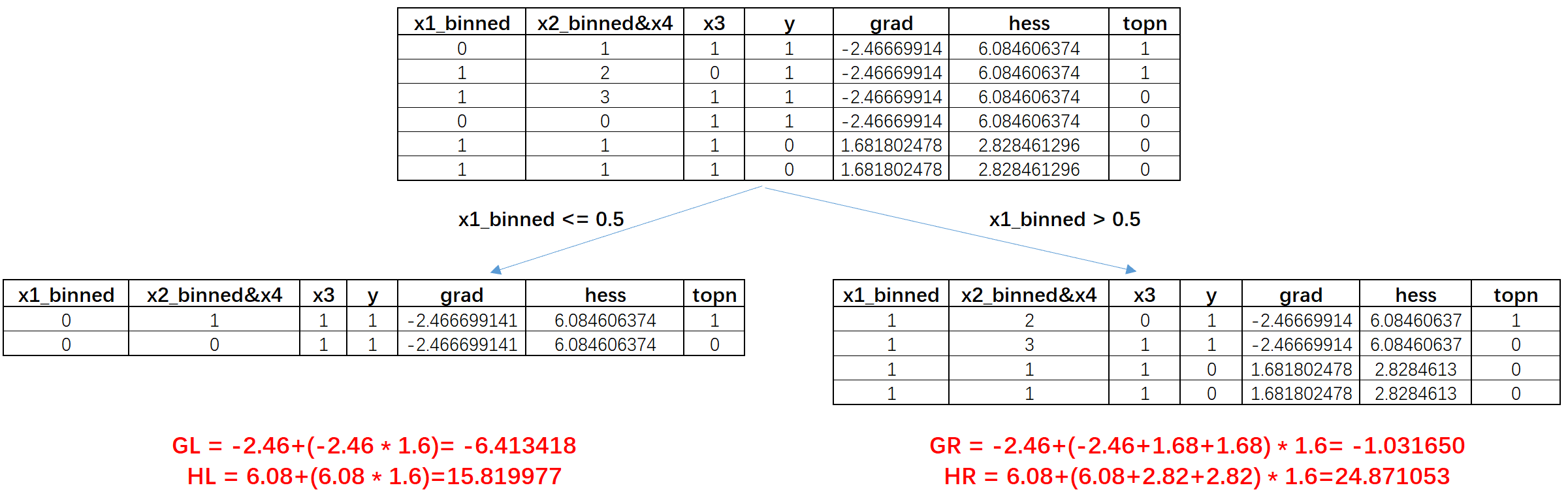
其中GL、HL代表左节点的梯度和及hess和，这里乘以的1.6实际上就是膨胀系数，在之前的GOSS采样过程中，top_rate=0.2，other_rate=0.5，因此膨胀系数$\theta = \frac{1-0.2}{0.5}=1.6$，所以我们在计算梯度和及hess和的时候需要把小样本先乘以膨胀系数再和大样本的结果进行相加。对应的GR、HR则代表右边节点的计算结果，在进行子数据集的梯度和及hess和的计算时，我们可以按照原始计算公式把每个子节点的grad和hess带入进行加权计算（小梯度样本需要乘以权重，再和大梯度样本进行求和），此时$GL=-6.413,HL=15.819,GR=-1.031,HR=24.87$，带入计算公式得出此时决策树分裂增益为：

$$Gain_{(x1\_binned=0.5)} = \frac{(-6.4)^2}{15.8 + 0.1} + \frac{(-1.031)^2}{24.87 + 0.1} - \frac{(-6.4 - 1.03)^2}{15.81 + 24.84 + 0.1}-0.02(\frac{6.48}{15.81+0.1}+\frac{1.031}{24.87+0.1})=1.2533$$

类似的我们可以继续计算其他备选切分点的增益，这里我们可以通过定义如下函数进行快速的分裂增益计算：

# 获取所有特征列
features = ['x1_binned', 'x2_binned&x4', 'x3']

# 计算备选切分点
split_candidates = {}
for feature in features:
    unique_values = data_goss[feature].unique()
    unique_values.sort()
    if len(unique_values) > 1:
        split_candidates[feature] = [(unique_values[i] + unique_values[i + 1]) / 2 for i in range(len(unique_values) - 1)]

print("备选切分点：", split_candidates)

备选切分点： {'x1_binned': [0.5], 'x2_binned&x4': [0.5, 1.5, 2.5], 'x3': [0.5]}

def calculate_gain(g_left, h_left, g_right, h_right, reg_alpha, reg_lambda):
    w_left = -g_left / (h_left + reg_lambda)
    w_right = -g_right / (h_right + reg_lambda)
    
    gain = (g_left ** 2) / (h_left + reg_lambda) + (g_right ** 2) / (h_right + reg_lambda) \
           - ((g_left + g_right) ** 2) / (h_left + h_right + reg_lambda) \
           - reg_alpha * (abs(w_left) + abs(w_right))
    return gain


def calculate_split_gain(data, feature, split_value, reg_alpha, reg_lambda):
    left_mask = data[feature] <= split_value
    right_mask = ~left_mask
    
    left_data = data[left_mask]
    right_data = data[right_mask]
    
    g_left = left_data.loc[left_data['topn'] == 1, 'grad'].sum() + left_data.loc[left_data['topn'] == 0, 'grad'].sum() * 1.6
    h_left = left_data.loc[left_data['topn'] == 1, 'hess'].sum() + left_data.loc[left_data['topn'] == 0, 'hess'].sum() * 1.6
    
    g_right = right_data.loc[right_data['topn'] == 1, 'grad'].sum() + right_data.loc[right_data['topn'] == 0, 'grad'].sum() * 1.6
    h_right = right_data.loc[right_data['topn'] == 1, 'hess'].sum() + right_data.loc[right_data['topn'] == 0, 'hess'].sum() * 1.6
    
    gain = calculate_gain(g_left, h_left, g_right, h_right, reg_alpha, reg_lambda)
    return gain


reg_alpha = 0.02
reg_lambda = 0.1

gain_results = {}

for feature, split_values in split_candidates.items():
    gain_results[feature] = []
    for split_value in split_values:
        gain = calculate_split_gain(data_goss, feature, split_value, reg_alpha, reg_lambda)
        gain_results[feature].append((split_value, gain))

print("分裂增益：")
for feature, gains in gain_results.items():
    print(f"{feature}: {gains}")

分裂增益：
x1_binned: [(0.5, 1.2585521787597664)]
x2_binned&x4: [(0.5, 0.6086807629778319), (1.5, 1.2585521787597664), (2.5, 0.6086807629778319)]
x3: [(0.5, 0.32823985769231157)]

能够发现，x1_binned=0.5和x2_binned&x4=2.5分裂增益相同，从算法原理来说此时会随机选取一个点作为分裂点，这里我们就假设以x1_binned=0.5作为第一层的分裂点进行决策树生长，考虑决策树的进一步生长策略。此时我们假设决策树经过第一层生长，分裂的两个子数据集分别为data_goss_1和data_goss_2，两个子数据集如下：

data_goss_1 = data_goss.loc[data_goss['x1_binned']==0]
data_goss_1

	x1_binned	x2_binned&x4	x3	y	grad	hess	topn
0	0.0	1.0	1	1	-2.466699	6.084606	1
8	0.0	0.0	1	1	-2.466699	6.084606	0

data_goss_2 = data_goss.loc[data_goss['x1_binned']==1]
data_goss_2

	x1_binned	x2_binned&x4	x3	y	grad	hess	topn
2	1.0	2.0	0	1	-2.466699	6.084606	1
5	1.0	3.0	1	1	-2.466699	6.084606	0
1	1.0	1.0	1	0	1.681802	2.828461	0
3	1.0	1.0	1	0	1.681802	2.828461	0

接下来我们即可继续围绕这两个子数据集进一步探讨决策树下一步生长过程。

• Leaf wise tree growth生长策略

  由于LGBM决策树算法是采用的Leaf wise tree growth生长策略，因此我们需要对比左、右子树各自的分裂增益，然后选择某一边进行进一步生长。这里左子树对应数据集data_goss_1，右子树对应data_goss_2数据集，很明显对于data_goss_1数据集来说，标签纯度已经达到100%，没有再分裂的必要，因此接下来重点考察右子树data_goss_2的分裂情况。通过观察我们不难发现，data_goss_2在x2_binned&x4=1.5切分点上，能够使得切分子数据集的标签纯度达到100%，因此我们手动尝试围绕这个点进行切分生长，并计算分裂增益。分裂过程如下：

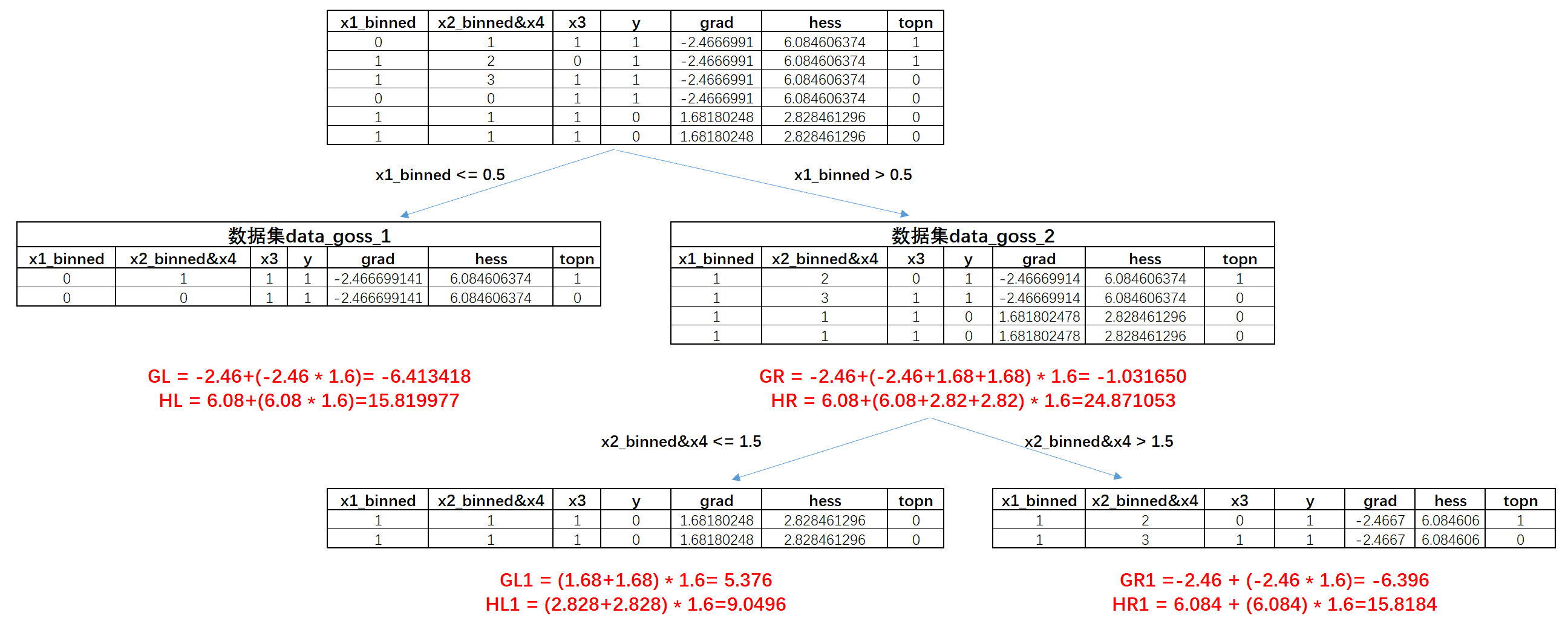
类似的我们先尝试进行手动计算，根据每个数据集的grad和hess，我们可以计算目前两个左右节点各自的梯度和及hess和，其中$GL1=5.376$，$HL1=9.0496$，$GR1=-6.396$，$HR1=15.8184$，然后带入增益公式：

$$Gain = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \alpha \cdot (|w_L|+|w_R|)$$

算得此时增益为：$Gain_{(x2\_binned \& x4=1.5)}=5.6862$

  当然，我们也可以借助此前定义的calculate_split_gain函数，快速的计算data_goss_2数据集中全部备选切分点的增益，得到结果如下：

reg_alpha = 0.02
reg_lambda = 0.1

gain_results = {}

for feature, split_values in split_candidates.items():
    gain_results[feature] = []
    for split_value in split_values:
        gain = calculate_split_gain(data_goss_2, feature, split_value, reg_alpha, reg_lambda)
        gain_results[feature].append((split_value, gain))

print("分裂增益：")
for feature, gains in gain_results.items():
    print(f"{feature}: {gains}")

分裂增益：
x1_binned: [(0.5, -0.0008262766087664918)]
x2_binned&x4: [(0.5, -0.0008262766087664918), (1.5, 5.686256576568045), (2.5, 2.0870031523895443)]
x3: [(0.5, 1.0407519630596518)]

能够发现，确实𝑥2_𝑏𝑖𝑛𝑛𝑒𝑑&𝑥4=1.5增益是最高的，因此，这层决策树将按照该切分点进行分裂生长。而生长后的决策树全部叶节点的标签纯度都达到了100%，因此不用再进行分裂，这颗决策树的生长到此结束。同时，我们也确实发现该决策树最终左右两边的子树深度并不相同，这也从侧面说明当前决策树是按照Leaf wise tree growth进行生长。

• 直方图差加速

  不难看出，尽管LGBM的决策树生长流程并不复杂，但针对每个备选节点的分裂增益的计算过程却略显繁琐，其中最繁琐的地方在于子数据集的grad和及hess和的计算过程，更具体的来说，繁琐之处在于需要区分大梯度样本和小梯度样本，然后赋予不同的权重进行求和，这个大小梯度样本的检索过程在实际计算机执行过程中是极耗费计算量的。

  而为了能够加速子样本的梯度和、hess和的计算过程，LGBM提出了基于梯度和及hess和的直方图优化算法，该算法首先要求用直方图来表示各数据集的梯度和、hess和的累计值，然后从数学层面可以非常简单的证明，在决策树分裂过程中梯度和、hess和整体累计值不变，因此子节点的梯度和、hess和的累计值将和父节点相同，进而在决策树分裂过程中，我们只需要计算父节点和左子树的梯度和、hess和，就能通过相减的方式得到右子树的梯度和、hess和。由此我们就可以摆脱每个节点独立计算梯度和、hess和的计算过程，进而大幅提升决策树建模过程中分裂增益的计算速度、从而加快决策树的建模效率。这个过程也就是直方图优化算法中的差加速优化。

  不难发现，直方图优化的过程涉及两个核心的技术要点，其一是要对每个数据集进行直方图转化，其二则是通过减法求得右子树的直方图。接下来我们尝试通过直方图优化算法来再执行一遍此前决策树模型的生长过程，通过对比来查看直方图具体加速过程的体现。

  首先需要计算和绘制根节点的直方图，这里的直方图指的是数据集中各变量取不同值时对应的样本的grad和及hess和，例如根节点来说，对于data_goss数据集中x1_binned这一列，0值样本如下：

data_goss[data_goss['x1_binned'] == 0]

	x1_binned	x2_binned&x4	x3	y	grad	hess	topn
0	0.0	1.0	1	1	-2.466699	6.084606	1
8	0.0	0.0	1	1	-2.466699	6.084606	0

其中0号样本是大梯度样本，而8号样本是小梯度样本。考虑到此时因此top_rate=0.2，other_rate=0.5，因此膨胀系数$\theta = \frac{1-0.2}{0.5}=1.6$，因此x1_binned中0值样本的梯度累加计算过程为0号样本梯度值+$\theta$ * 8号样本梯度值，计算结果如下：

-2.466699 + (-2.466699) * 1.6

-6.4134174

x1_binned=0的样本对应的hess值也是类似的计算过程：

6.084606 + (6.084606) * 1.6

15.8199756

类似的我们可以计算x1_binned=1对应的样本的梯度和以及hess和：

data_goss[data_goss['x1_binned'] == 1]

	x1_binned	x2_binned&x4	x3	y	grad	hess	topn
2	1.0	2.0	0	1	-2.466699	6.084606	1
5	1.0	3.0	1	1	-2.466699	6.084606	0
1	1.0	1.0	1	0	1.681802	2.828461	0
3	1.0	1.0	1	0	1.681802	2.828461	0

# 梯度和
-2.466699 + (-2.466699 + 1.681802 + 1.681802) * 1.6

-1.0316510000000003

# hess和
6.084606 + (6.084606 + 2.828461 + 2.828461) * 1.6

24.8710508

据此，我们就可以将x1_binned用下图的直方图进行表示，其中直方图的不同柱子用于表示x1_binned特征不同取值下累计的梯度（也就是梯度和）和累计的hess（Hessian和），注意，这个累加的过程就是数值累加，而非绝对值累加：

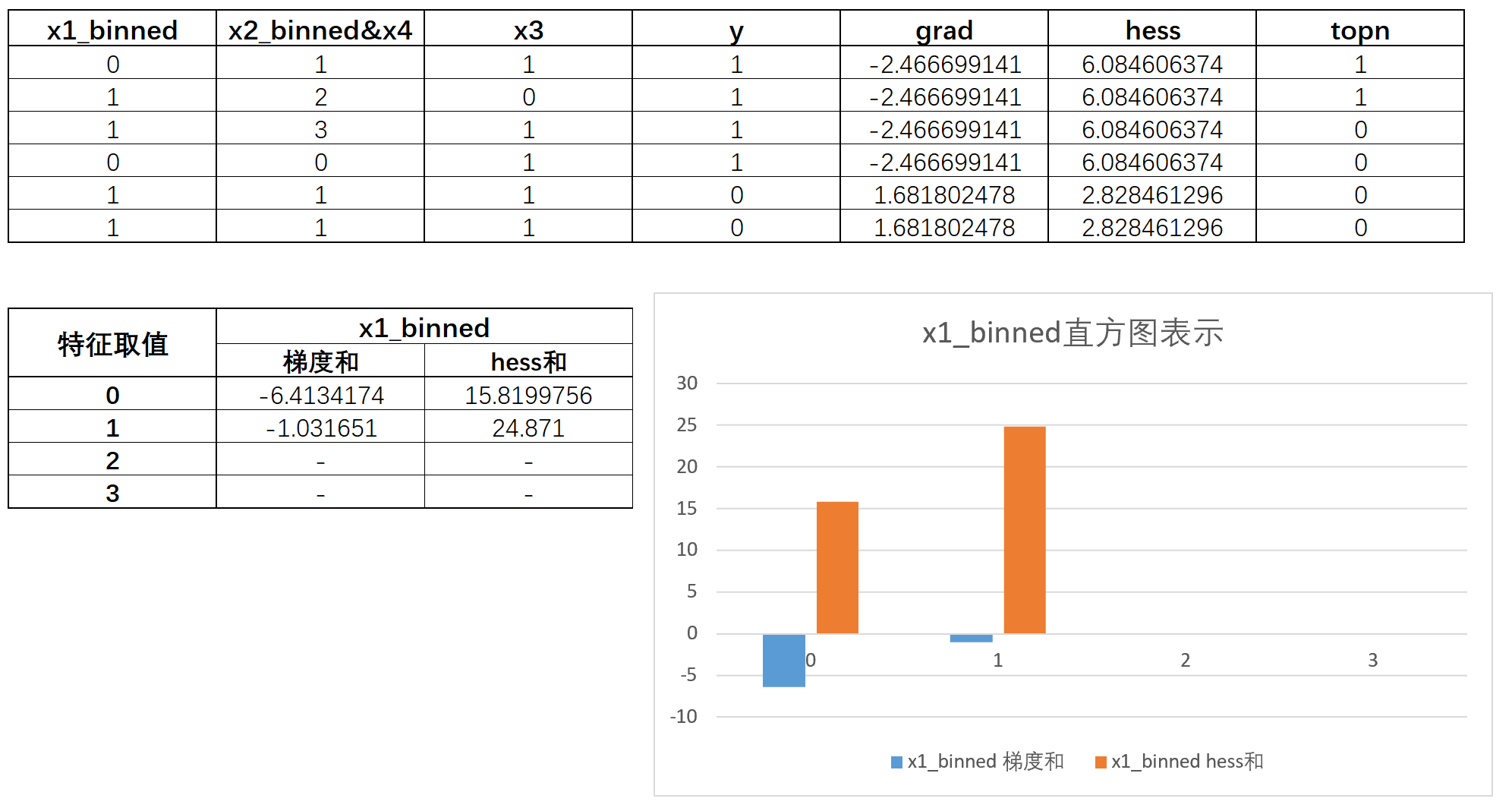
对应的，我们还需要计算其他特征在不同取值下，对应的数据集的梯度和以及hess和，相关计算我们可以通过如下代码实现：

import pandas as pd

# 按照 x1_binned 分组
groups = data_goss.groupby('x1_binned')

# 定义聚合函数
agg_func = lambda x: pd.Series({
    'grad_sum': x[x['topn']==1]['grad'].sum() + 1.6 * x[x['topn']==0]['grad'].sum(),
    'hess_sum': x[x['topn']==1]['hess'].sum() + 1.6 * x[x['topn']==0]['hess'].sum(),
})

# 对每个分组应用聚合函数
result_x1 = groups.apply(agg_func).reset_index()

# 按照 x2_binned&x4 分组
groups = data_goss.groupby('x2_binned&x4')

# 对每个分组应用聚合函数
result_x2_x4 = groups.apply(agg_func).reset_index()

# 按照 x3 分组
groups = data_goss.groupby('x3')

# 对每个分组应用聚合函数
result_x3 = groups.apply(agg_func).reset_index()

其中groupby、apply等方法我们在特征工程Part2、3中曾有详细介绍，这里我们不再进行赘述。验证计算结果如下：

result_x1

	x1_binned	grad_sum	hess_sum
0	0.0	-6.413418	15.819977
1	1.0	-1.031650	24.871053

result_x2_x4

	x2_binned&x4	grad_sum	hess_sum
0	0.0	-3.946719	9.735370
1	1.0	2.915069	15.135683
2	2.0	-2.466699	6.084606
3	3.0	-3.946719	9.735370

result_x3

	x3	grad_sum	hess_sum
0	0	-2.466699	6.084606
1	1	-4.978368	34.606423

据此，我们绘制整个根节点的直方图如下：

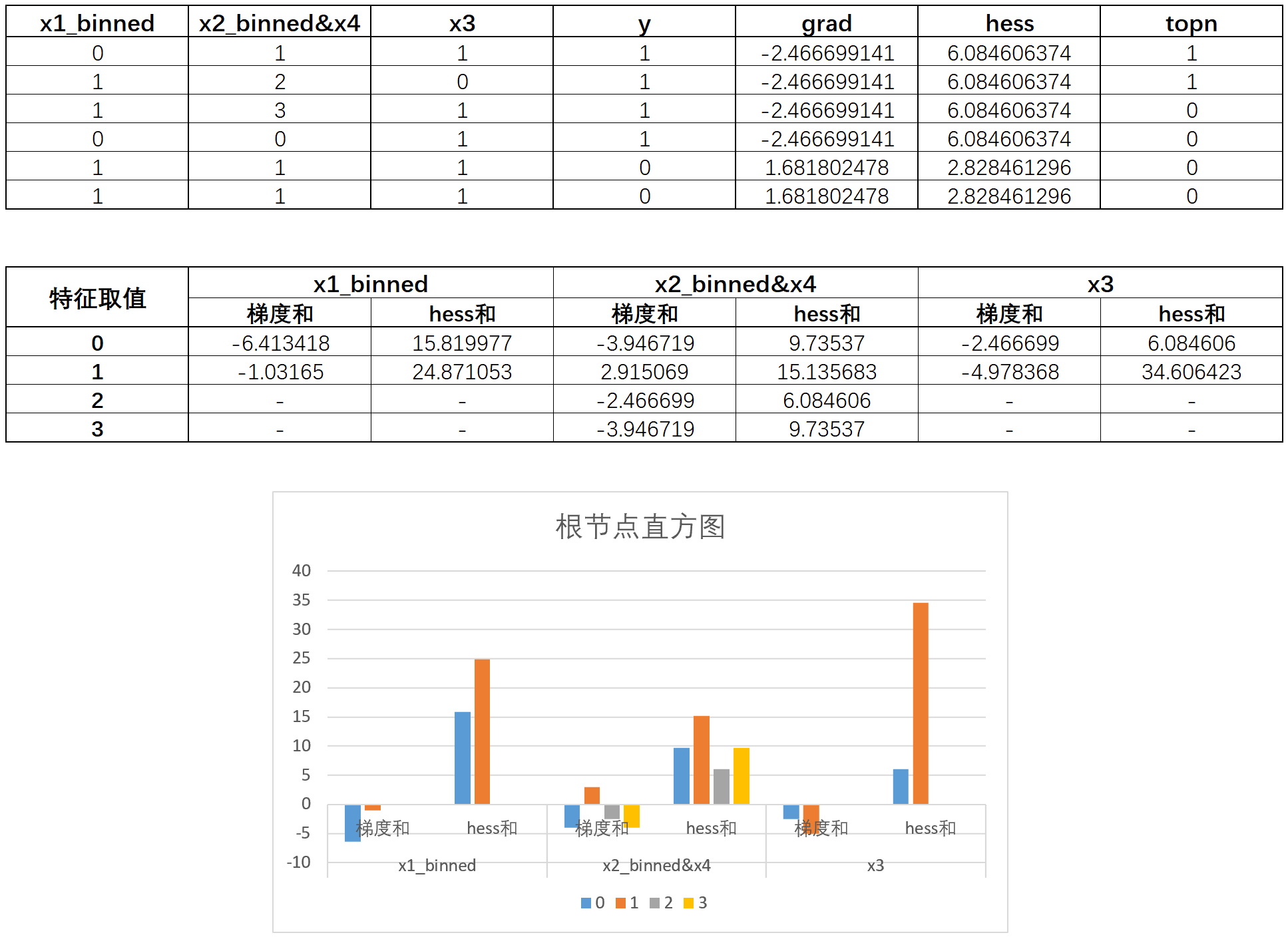
然后我们来进行第一次分裂，之前我们首先尝试了x1_binned=0.5为切分点进行分裂，分裂结果如下：

此时我们不难发现，$GL$、$HL$、$GR$、$HR$实际上就是根节点中result_x1的计算结果：

result_x1

	x1_binned	grad_sum	hess_sum
0	0.0	-6.413418	15.819977
1	1.0	-1.031650	24.871053

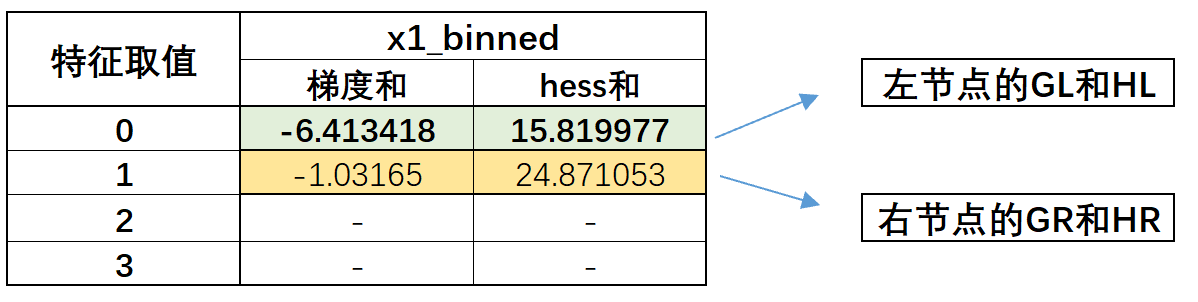
因此，如果此前计算过根节点的直方图，就能够非常快速的直接得出现在的子节点的梯度和及hess和。当然，当我们得到两个子节点之后，我们需要围绕这两个数据集分别再进行直方图计算，即不同特征取值下对应的grad和及hess和，并且这里其实我们只需要计算左节点的直方图，右节点的直方图可以通过父节点减去左节点直方图直接计算得到，例如此时左节点的直方图如下：

data_goss_1

	x1_binned	x2_binned&x4	x3	y	grad	hess	topn
0	0.0	1.0	1	1	-2.466699	6.084606	1
8	0.0	0.0	1	1	-2.466699	6.084606	0

groups = data_goss_1.groupby('x1_binned')

# 对每个分组应用聚合函数
result_x1 = groups.apply(agg_func).reset_index()

# 按照 x2_binned&x4 分组
groups = data_goss_1.groupby('x2_binned&x4')

# 对每个分组应用聚合函数
result_x2_x4 = groups.apply(agg_func).reset_index()

# 按照 x3 分组
groups = data_goss_1.groupby('x3')

# 对每个分组应用聚合函数
result_x3 = groups.apply(agg_func).reset_index()

result_x1

	x1_binned	grad_sum	hess_sum
0	0.0	-6.413418	15.819977

result_x2_x4

	x2_binned&x4	grad_sum	hess_sum
0	0.0	-3.946719	9.735370
1	1.0	-2.466699	6.084606

result_x3

	x3	grad_sum	hess_sum
0	1	-6.413418	15.819977

而右节点直方图，则可以利用父节点直方图直接减去左节点直方图得到：

而这个详见的过程其实非常简单，就是对应位置梯度和及hess和相减即可。

而我们完成左右子节点的直方图计算后，即可继续计算不同切分点的分裂增益，同样，由于我们已经得到data_goss_1和data_goss_2两个数据集的直方图，因此这两个数据集的分裂增益计算过程也将变得非常简单，例如我们这里仍然以右节点的x2_binned&x4=1.5为切分点，计算分裂增益，此时的分裂增益计算过类似于根节点的第一次分裂过程，我们只需要根据data_goss_2的直方图就能快速得到分裂子节点的GL1、HL1、GR1和HR1：

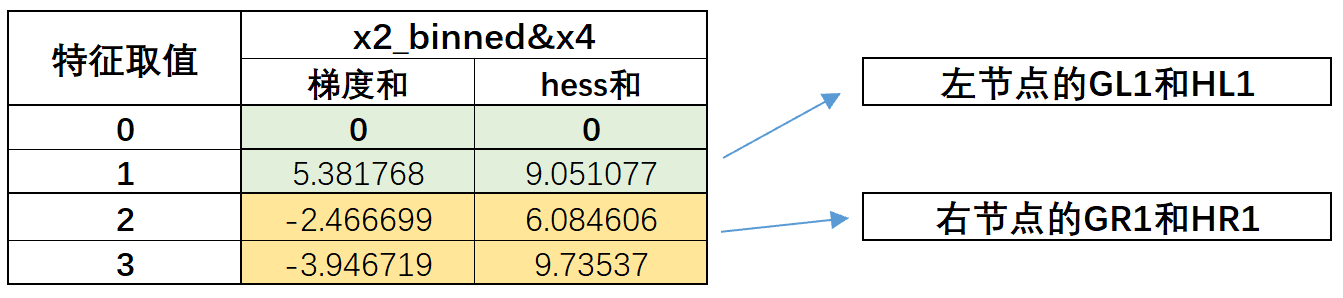
此时GL1=5.38，HL1=9.05，GR1=(-2.46-3.946)=-6.396，HR1=6.084+9.73=15.81。然后就可依据这个结果快速计算分裂增益。这里可以对比此前我们手动计算的结果来验证直方图计算结果是否正确：

能够发现，直方图优化算法的计算结果和手动计算结果一致。从而也验证了直方图优化算法本身的正确性。

• 直方图优化算法的有效性讨论

  从本质上来说，直方图优化其实是提供了一种特殊的能够保存数据集梯度累加和hess累加的对象（一下简称为直方图对象），然后在决策树的分裂增益计算过程中通过减法计算代替一个节点的梯度和及hess和的计算过程。这个过程看似减少的计算不多，但实际上LGBM算法在实际创建直方图对象的过程中会有非常多的数据类型优化方法，能够进一步加快这个计算过程。同时，哪怕在单次计算中看似提升不大的方法，在海量数据处理时都能带来巨大的计算时间减少。实际上，根据官方说明文档的论述，直方图优化为决策树生长的计算过程了节约了40%的计算时间。

  至此，我们就完整介绍了LGBM算法中单独一颗决策树的建模过程。下一小节我们将在这两个小节介绍的基本原理基础之上，来进行完整的LGBM迭代过程的数学推导，帮大家从更加宏观的层面掌握LGBM迭代流程。